Rearranging a Formula
Sometimes you need to substitute terms in a formula. The formula below is a common formula used to find the area of a circle.
Area, sq ft = 3.14 X R X R where R is Radius
However, you may be given the diameter rather than the radius. Given the diameter, you could divide it by 2 since, the radius is half the diameter.
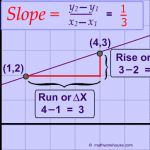
Another formula that is used often in collection system calculations is to find the Slope:
Slope = (Rise) / (Run)
Slope is defined as Rise/Run (the upward rise divided by the length of the run). Because the rise is less than the run, slope is a decimal number – always less than one. Often, one wants to know the percent slope. Remember, to change a decimal number to a percent, you must multiply by 100. Whatever you do to one side of a formula, you must do to the other. So the formula is:
Slope X 100 = (Rise) / (Run) X 100 OR Slope (%) = (Rise) / (Run) X 100
When using a formula to solve problems, take care to rearrange the formula correctly. If you must use several steps to do it, show these steps in your work so you can go back and see what you did. If you can’t rearrange a formula correctly, you can’t get a correct answer.
Don’t forget that to get your final answer in the correct units, you may need to use one or more conversion factors!
Examples:
1. A 1000-foot pipe with a 2.0% slope enters a lift station at an invert elevation of 940.0 feet. What is the elevation at the other end of the pipe?
Formula: Slope % = (Rise) / (Run) X 100
2. What is the loading, in pounds/day, of wastewater with a strength of 500 mg/L and a flow rate of 0.89 million gallons/day?
Formula: Loading = Flow, MGD X Concentration, mg/L X 8.34 lbs/gal
Answers:
1. Slope (%) = (Rise) / (Run) X 100
Rearrange the formula: Rise = (Slope % X Run) / (100)
Rise = (2.0 % X 1000 ft) / (100) = 20 feet
Dividing % by 100 changes the number to a decimal
Elevation (Final) = Elevation (initial) + Rise
Elevation (Final) = 940 feet + 20 feet
Elevation (Final) = 960 ft
2. It is important to note that 1 mg/L is equal to 1 part per million (1 part/1 million parts). In this example, to show that units cancel, will us use as a conversion factor a compound fraction – which is resolved by inverting the denominator and multiplying as shown in the second step.
Loading = (500 mg X 0.89 million gal X 8.34 lb X 1 part/million parts) / (L X day X gallon X 1 mg/L)
(500 mg) X (0.89 million gal) X (8.34 lb) X (1 part / million parts)
(L) X (day) X (gallons) X (1 mg/L)
Loading = 3711.3 lb/day
Or you can use the Davidson Pie Chart for any Loading Formula: